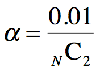3つ以上のデータ群がお互いに異なる母集団に由来するのか、それとも同じ母集団に由来するのがわからない...
2つのデータ群が異なる母集団由来と見なしてよいか、あるいは同一母集団由来と見なすべきかを検定するためにt検定を用いた。一般に統計検定では、本来は同一なのに間違えて別の集団と判断してしまう危険(帰無仮説を誤って棄却:第一種の誤り)と、本来は別の集団のはずなのに間違えて同一集団と見なしてしまう危険(帰無仮説を誤って採択:第二種の誤り)とが存在する。有意水準を5%と1%の違いは、第一種の誤りと第二種の誤りとでどちらにより気をつけるかの違いであるとも言える。5%と1%の違いは、t分布における両末端(または片側末端)部分の面積の違いであり、1%の方が5%よりも面積が狭いので、1%の方が帰無仮説を誤って棄却する場合が少ない。言い換えると帰無仮説に対して保守的である(帰無仮説をなかなか破棄しようとはしない)。そのことは同時に、帰無仮説を誤って採択する場合が多くなる(第二種誤りの可能性を増加)ことを意味する。1%有意水準の場合は、観測された現象が帰無仮説に従っていたとしても、たまたま101回に1回程度しか発生しない現象を観測してしまったならば、帰無仮説を破棄されてしまう。5%有意水準の場合は、観測された現象が21回中1回程度しか発生しない現象ならば、帰無仮説は破棄されてしまう。
さて、3つのデータ群において、これらのデータ群が同一の母集団由来なのか、異なる母集団由来なのかを検定する必要が出てくることもあろう。3つとは限らずN個のデータ群においても同様な検定が必要になってくることがある。この場合に任意の2群を取ってきて、それぞれのデータ群ペアにおいて、データの平均値が統計的に同じであるという帰無仮説を立て、普通にt検定をすればよいように思える。3つのデータ群の場合、任意の2群を取ってくる場合の数は、3であるので、3回t検定をすればよいことになる。ここで注意すべきことは、検定の有意水準である。有意水準を5%にした場合、統計的には20回に1回は誤った判断をする可能性がある。3つのデータ群が同一の母集団由来であるならば、この3つのデータ群が同一母集団由来であると正しく判断できる確率は、

3個以上のデータ群の差を検定する場合には、全体を1回で検定する必要がある。すべてのデータ群が同一の母集団由来と見なせるか、あるいは少なくともひとつのデータ群は異なる母集団由来かを検定する。つまり、各データ群から得られる平均値がすべて等しいという帰無仮説を棄却できるかどうかを検定する。この検定では、各データ群の平均値のまわりでのばらつきが、全データのばらつきと同程度かどうかを調べる。
N個のデータ群がある時に、それぞれの群のデータの平均値をμk (k = 1,2,3,...N) とする。またそれぞれの推定分散をskとする。これらから、全データのばらつきは以下の式で推定できる。

全データのばらつきを直接推定するには、全データの平均値と分散がわかればよい。

上記2つの値を割った値、つまりF分布にしたがうことがわかっている。

ここにあげた評価方法は、分散分析(analysis of variance)、または英語の頭文字を取ってANOVAとよばれている。
分散分析によって、すべてのデータが同一母集団由来ではないことがわかった場合(帰無仮説が破棄された場合)、どの群が異なっているかを知る必要がある。それには、データ群ペアでt検定を実行する必要が出てくる。しかし各t検定における有意水準が問題になる。一番最初の問題に戻ってきてしまった。この事態を回避するには、それぞれのt検定における有意水準を小さくすればよい。有意水準をどの程度のすればよいかを決める方法として、Bonferroniの調整法が知られている。N個のデータ群において、全体の有意水準を0.01にしたければ、それぞれのt検定における有意水準を以下の式で決まるαの値にすればよい。