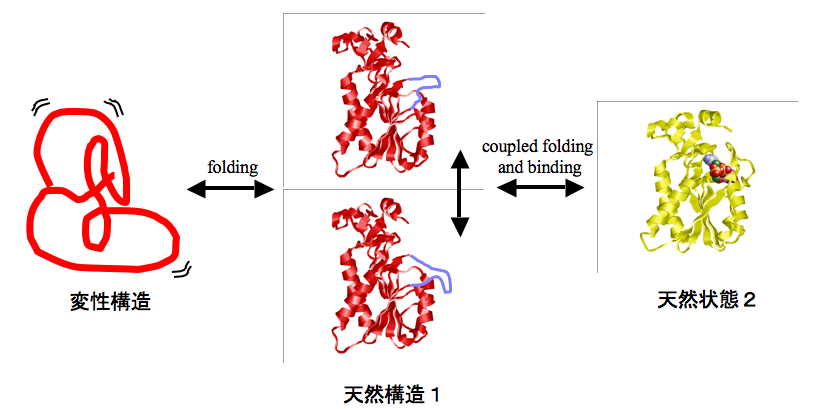
非構造領域のアミノ酸配列を観察すると、出現するアミノ酸残基の種類が乏しい(同じアミノ酸残基が繰り返しあらわれる)傾向にある。 この傾向を数値化することで、非構造領域を推定することができるかもしれない。
アミノ酸残基数W個からなる領域を観測したときに、その中に存在するアミノ酸残基の順番を入れ替えて構築できるすべてのアミノ酸配列の うち、観測されているアミノ酸配列と同じアミノ酸配列がどの程度含まれているかを計算すると、今見ているW個の領域がどの程度複雑かがわかる。 例えば、W個の中がすべてアラニンならば、アミノ酸残基の順番をいくら変えても、すべてのアミノ酸配列が観測されている配列とまったく同じで ある。

この計算のプログラムは、以下のようになる;
/******************************************************************************/
#include < stdio.h >
#include < stdlib.h >
#include < string.h >
#include < math.h >
#define MAXLOG 40
#define PAI 3.1415926
#define MAXSEQ 1000
int W;
static char aa1[] = "ACDEFGHIKLMNPQRSTVWY";
static double log2fac[MAXLOG] = {0.0, 0.0, 1.0, 2.584963, 4.584963,
6.906891, 9.491853, 12.29921, 15.29921,
18.46913, 21.79106, 25.25049, 28.83546,
32.53589, 36.34325, 40.25014, 44.25014,
48.33760, 52.50753, 56.75546, 61.07738,
65.46987, 69.92913, 74.45269, 79.03766,
83.68151, 88.38195, 93.13684, 97.94420,
102.8022, 107.7091, 112.6632, 117.6633,
122.7077, 127.7951, 132.9244, 138.0943,
143.3037, 148.5517, 153.8371};
/******************************************************************************/
double logfac(x)
int x;
{
double coef;
if (x < 10)
return(log2fac[x]);
else {
coef = 1.0/log(2.0); /* 1.442695 */
return(coef* ((x+0.5)*log((double)x)
- x
+ 0.5*log(2.0*PAI)
+ 1.0/(12.0*x)));
}
}
/******************************************************************************/
/******************************************************************************/
void complex(len,seq,complexity)
int len;
char seq[MAXSEQ];
double complexity[MAXSEQ];
{
int i, j, k;
double K, Kint;
double Kave;
double coef;
int aa[20];
double logfac();
coef = 1.0/log(2.0); /* 1.442695 */
Kint = logfac(W);
Kave = 2.00;
for (j = 0; j < 20; j++)
aa[j] = 0;
for (j = 0; j < len; j++)
complexity[j] = Kave;
for (j = 0; j < W; j++)
for (k = 0; k < 20; k++)
if (seq[j] == aa1[k]) {
aa[k]++;
break;
}
K = 0.0;
for (k = 0; k < 20; k++)
K += logfac(aa[k]);
complexity[W/2] = (Kint - K)/(double)W;
for (j = W/2+1; j < len-W/2; j++) {
for (k = 0; k < 20; k++)
if (seq[j-1-W/2] == aa1[k]) {
aa[k]--;
break;
}
for (k = 0; k < 20; k++)
if (seq[j+W/2] == aa1[k]) {
aa[k]++;
break;
}
K = 0.0;
for (k = 0; k < 20; k++)
K += logfac(aa[k]);
complexity[j] = (Kint - K)/(double)W;
}
return;
}
/******************************************************************************/
/******************************************************************************/
FILE *openfile(filename)
char *filename;
{
FILE *fp;
if ((fp = fopen(filename,"r")) == NULL) {
fprintf(stderr,"Cannot open %s\n",filename);
exit (-1);
}
return(fp);
}
/******************************************************************************/
/******************************************************************************/
int readseq(fp,seq)
FILE *fp;
char seq[];
{
int c;
int i;
i = 0;
while((c = getc(fp)) != EOF) {
if (c == ' ') continue;
if (c == '\n') continue;
seq[i++] = c;
if (i > MAXSEQ) {
fprintf(stderr,"Increase MAXSEQ\n");
exit (-1);
}
}
return(i);
}
/******************************************************************************/
/******************************************************************************/
main(argc, argv)
int argc;
char *argv[];
{
int i, len;
char seq[MAXSEQ];
double complexity[MAXSEQ];
FILE *fp;
void complex();
FILE *openfile();
if (argc < 2) {
fprintf(stderr, "%s (seq) \n",argv[0]);
exit (-1);
}
W = 13;
fp = openfile(argv[1]);
len = readseq(fp,seq);
fclose(fp);
complex(len,seq,complexity);
for (i = 0; i < len; i++)
printf("%c %10.4f\n",seq[i],complexity[i]);
return;
}
/* EOF */
このプログラムはフリーフォーマット(以下の問題にあるアミノ酸配列のフォーマット)のファイルを入力として、1行にアミノ酸1残基とその残基付近の複雑度値を出力する。
結果を表計算ソフトウエアに取り込むと簡単にグラフを描くことができる。
MQGSVTEFLKPRLVDIEQVSSTHAKVTLEPLERGFGHTLGNALRRILLSSMPGCAVTEVEIDGVLHEYSTKEGVQEDILEILLNLKGLAVRVQGKDEVILTLNKSGIGPVTAADITHDGD VEIVKPQHVICHLTDENASISMRIKVQRGRGYVPASTRIHSEEDERPIGRLLVDACYSPVERIAYNVEAARVEQRTDLDKLVIEMETNGTIDPEEAIRRAATILAEQLEAFVDLRDVRQP EVKEEKPEFDPILLRPVDDLELTVRSANCLKAEAIHYIGDLVQRTEVELLKTPNLGKKSLTEIKDVLASRGLSLGMRLENWPPASIADE